Transductive Learning for Textual Few-Shot Classification: API-based Few-shot Learning

Table of Links

• Abstract & Introduction
• Related Work
• API-based Few-shot Learning
• An Enhanced Experimental Setting
• Experiments
• Conclusions
• Limitations, Acknowledgements, & References
• Appendix A: Proof of Proposition
• Appendix B: Additional Experimental Results

3 API-based Few-shot Learning

3.1 Problem Statement

3.2 Proposed Transductive Method

NLP few-shot classifiers rely only on inductive inference, while computer vision has shown significant performance improvements using transductive inference for FSL. Transductive inference succeeds in FSL because it jointly classifies all unlabeled query samples of a single task, leading to more efficient and accurate classification compared to inductive methods that classify one sample at a time. Let us begin by introducing some basic notation and definitions before introducing our new transductive loss based on the Fisher-Rao distance.

Note that this transductive regularization has been proposed in the literature based on the InfoMax principle (Cardoso, 1997; Linsker, 1988), and the inductive loss can be found by setting λ = 0. In what follows, we review the regularizers introduced in previous work.

Entropic Minimization (H) An effective regularizer for transductive FSL can be derived from the field of semi-supervised learning, drawing inspiration from the approach introduced in (Grandvalet and Bengio, 2004). This regularizer, proposed in (Dhillon et al., 2019), utilizes the conditional Shannon Entropy (Cover, 1999) of forecast results from query samples during testing to enhance model generalization. Formally:

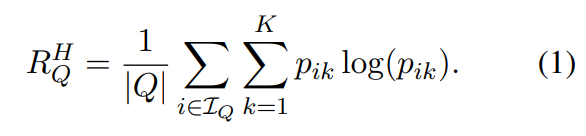
Limitation of existing strategies: Despite its effectiveness, the previous method has a few limitations that should be taken into account. One of these limitations is the need to fine-tune the weight of different entropies using the hyperparameter α. This parameter-tuning process can be time-consuming and may require extensive experimentation to achieve optimal results. Additionally, recent studies have shown that relying solely on the first Entropic term, which corresponds to the Entropic minimization scenario in Equation 1, can lead to suboptimal performance in FSL.

3.3 A Fisher-Rao Based Regularizer

In the FSL scenario, minimizing parameter tuning is crucial. Motivated by this, in this section, we introduce a new parameter-free transductive regularizer that fits into the InfoMax framework. Additionally, our loss inherits the attractive properties of the Fisher-Rao distance between soft-predictions q := (q1, . . . , qK) and p := (p1, . . . , pK), which is given by (Picot et al., 2023):

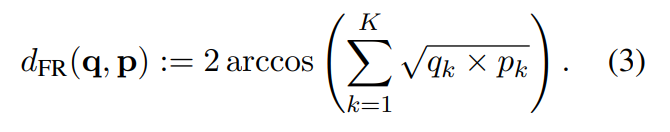
3.4 Additional Few-shot Inductive Baseline

In addition to the transductive methods of Sec. 3.2, we will explore three additional inductive methods for few-shot classification: prototypical networks, linear probing, and a semi-supervised classifier.

Prototypical Networks (PT) PT learn a metric space where the distance between two points corresponds to their degree of similarity. During inference, the distance between the query example and each class prototype is computed, and the predicted label is the class with the closest prototype. PT has been widely used in NLP and is considered as a strong baseline (Snell et al., 2017; Sun et al., 2019b; Gao et al., 2019).

Linear Probing (CE) Fine-tuning a linear head on top of a pretrained model is a popular approach to learn a classifier for classification tasks and was originally proposed in (Devlin et al., 2018).

Semi-supervised Baselines (SSL). We additionally propose two semi-supervised baselines following two steps. In the first step, a classifier is trained using the support set S and used to label Q. In the second step, the final classifier is trained on both S and Q with the pseudo label obtained from the first step.

[3] λ is set to 1 in all the experiments.