This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ulysse Gazin, Universit´e Paris Cit´e and Sorbonne Universit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation,
(2) Gilles Blanchard, Universit´e Paris Saclay, Institut Math´ematique d’Orsay,
(3) Etienne Roquain, Sorbonne Universit´e and Universit´e Paris Cit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation.
Table of Links
- Abstract & Introduction
- Main results
- Application to prediction intervals
- Application to novelty detection
- Conclusion, Acknowledgements and References
- Appendix A: Exact formulas for Pn,m
- Appendix B: Numerical bounds and templates
- Appendix C: Proof
- Appendix D: Explicit control of (16) for α=0
- Appendix E: Proof of Corollary 4.1
- Appendix F: The Simes inequality
- Appendix G: Uniform FDP bound for AdaDetect
- Appendix H: Additional experiments
4 Application to novelty detection
4.1 Setting
In the novelty detection problem, we observe the two following independent samples:


4.2 Adaptive scores
Following Bates et al. (2023); Marandon et al. (2022), we assume that scores are computed as follows:
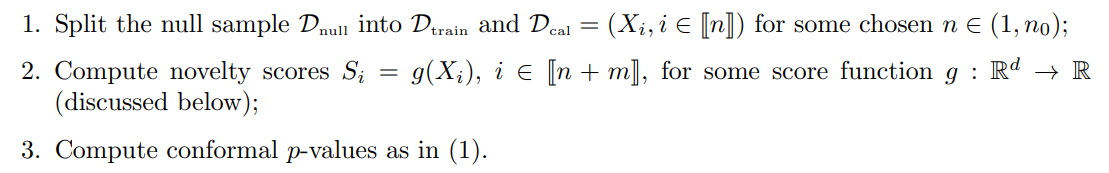
In the work of Bates et al. (2023), the score function is built from Dtrain only, using a one-class classification method (classifier solely based on null examples), which makes the scores independent conditional to Dtrain. The follow-up work Marandon et al. (2022) considers a score function depending both on Dtrain and Dcal ∪ Dtest (in a permutation-invariant way of the sample Dcal ∪ Dtest), which allows to use a two-class classification method including test examples. Doing so, the scores are adaptive to the form of the novelties present in the test sample, which significantly improves novelty detection (in a nutshell: it is much easier to detect an object when we have some examples of it). While the independence of the scores is lost, an appropriate exchangeability property is maintained so that we can apply our theory in that case, by assuming in addition (NoTies).
4.3 Methods and FDP bounds
Let us consider any thresholding novelty procedure
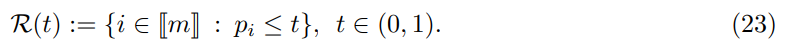
Then the following result holds true.
Corollary 4.1. In the above novelty detection setting and under Assumption NoTies, the family of thresholding novelty procedures (23) is such that, with probability at least 1 − δ, we have for all t ∈ (0, 1),
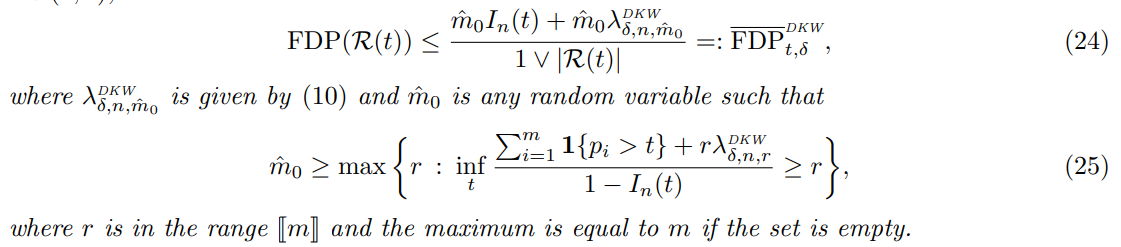
The proof is provided in Appendix E.
Remark 4.2. Among thresholding procedures (23), AdaDetect (Marandon et al., 2022) is obtained by applying the Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg, 1995) to the conformal p-values. It is proved to control the expectation of the FDP (that is, the false discovery rate, FDR) at level α. Applying Corollary 4.1 provides in addition an FDP bound for AdaDetect, uniform in α, see Appendix G.
4.4 Numerical experiments
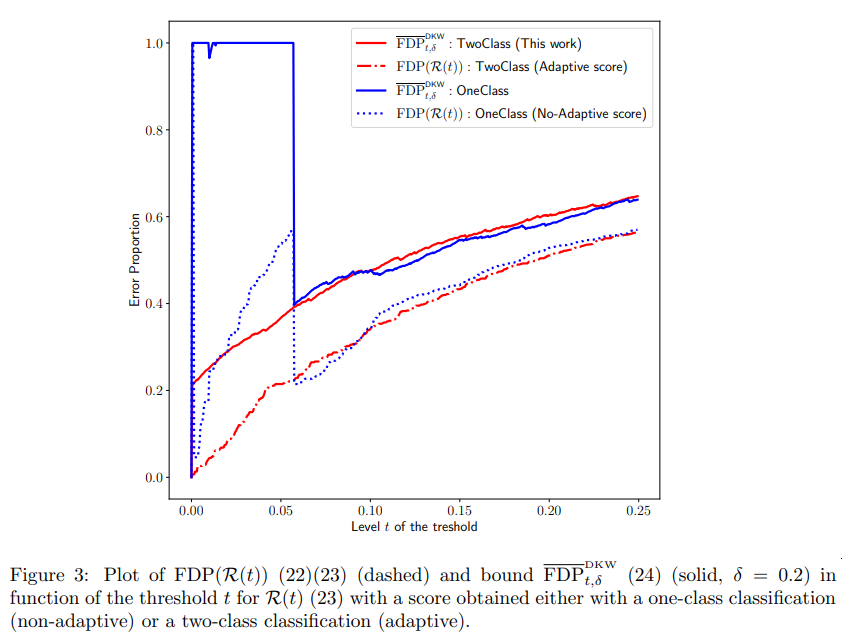
We follow the numerical experiments on “Shuttle” datasets of Marandon et al. (2022). In Figure 3, we displayed the true FDP and the corresponding bound (24) when computing p-values based on different scores: the non-adaptive scores of Bates et al. (2023) obtained with isolation forest oneclass classifier; and the adaptive scores of Marandon et al. (2022) obtained with random forest two-class classifier. While the advantage of considering adaptive scores is clear (smaller FDP and bound) , it illustrates that the bound is correct simultaneously on t. Additional experiments are provided in Appendix H.