This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ulysse Gazin, Universit´e Paris Cit´e and Sorbonne Universit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation;
(2) Gilles Blanchard, Universit´e Paris Saclay, Institut Math´ematique d’Orsay;
(3) Etienne Roquain, Sorbonne Universit´e and Universit´e Paris Cit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation.
Table of Links
- Abstract & Introduction
- Main results
- Application to prediction intervals
- Application to novelty detection
- Conclusion, Acknowledgements and References
- Appendix A: Exact formulas for Pn,m
- Appendix B: Numerical bounds and templates
- Appendix C: Proof
- Appendix D: Explicit control of (16) for α=0
- Appendix E: Proof of Corollary 4.1
- Appendix F: The Simes inequality
- Appendix G: Uniform FDP bound for AdaDetect
- Appendix H: Additional experiments
Abstract
Conformal inference is a fundamental and versatile tool that provides distribution-free guarantees for many machine learning tasks. We consider the transductive setting, where decisions are made on a test sample of m new points, giving rise to m conformal p-values. While classical results only concern their marginal distribution, we show that their joint distribution follows a P´olya urn model, and establish a concentration inequality for their empirical distribution function. The results hold for arbitrary exchangeable scores, including adaptive ones that can use the covariates of the test+calibration samples at training stage for increased accuracy. We demonstrate the usefulness of these theoretical results through uniform, inprobability guarantees for two machine learning tasks of current interest: interval prediction for transductive transfer learning and novelty detection based on two-class classification.
Keywords: Conformal inference, Multiple testing, False Discovery Rate, Uniform error control
1 Introduction
Conformal inference is a general framework aiming at providing sharp uncertainty quantification guarantees for the output of machine learning algorithms used as “black boxes”. A central tool of that field is the construction of a “(non)-conformity score” Si for each sample point. The score functions can be learnt on a training set using various machine learning methods depending on the task at hand. The scores observed on a data sample called “calibration sample” Dcal serve as references for the scores of a “test sample” Dtest (which may or may not be observed, depending on the setting). The central property of these scores is that they are an exchangeable family of random variables.
1.1 Motivating tasks
To be more concrete, we start with two specific settings serving both as motivation and as application.
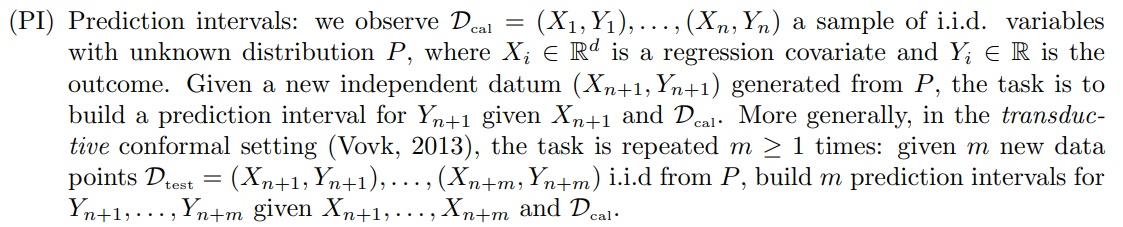

For both inference tasks, the usual pipeline is based on the construction of non-conformity real-valued scores S1, . . . , Sn+m for each member of Dcal ∪ Dtest, which requires an additional independent training sample Dtrain (in the so-called “split conformal” approach):
(PI) the scores are (for instance) the regression residuals Si = |Yi − µ(Xi ; Dtrain)|, 1 ≤ i ≤ n + m, where the function µ(x; Dtrain) is a point prediction of Yi given Xi = x, learnt from the sample Dtrain.
(ND) the scores are of the form Si = g(Xi ; Dtrain), 1 ≤ i ≤ n + m, where the score function g(·; Dtrain) is learnt using the sample Dtrain; g(x) is meant to be large if x is fairly different from the members of Dtrain (so that it is “not likely” to have been generated from P0).
In both cases, inference is based on the so-called split conformal p-values (Vovk et al., 2005):
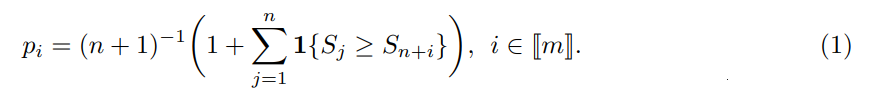
In other words, (n + 1)pi is equal to the rank of Sn+i in the set of values {S1, . . . , Sn, Sn+i}, and a small p-value pi indicates that the test score Sn+i is abnormally high within the set of reference scores. The link to the two above tasks is as follows: for (PI), the prediction interval C(α) for Yn+i with coverage probability (1 − α) is obtained by inverting the inequality pi > α w.r.t. Yn+i , see (13) below. For (ND), the members of the test sample declared as novelties are those with a p-value pi ≤ t for some threshold t.
Studying the behavior of the conformal p-value family is thus a cornerstone of conformal inference. Still, classical results only concern the marginal distribution of the p-values while the joint distribution remains largely unexplored in full generality.
1.2 Contributions and overview of the paper
In Section 2, we present new results for the joint distribution of the conformal p-values (1) for general exchangeable scores (for any sample sizes n and m). First, in Section 2.2, we show that the dependence structure involved only depends on n and m, and follows a P´olya urn model; this entails both explicit formula and useful characterizations. Second, we deduce a new finite sample DKWtype concentration inequality (Massart, 1990) for the empirical distribution function (ecdf) of the conformal p-values. We emphasize the following favorable features of our results for application of the conformal methodology:
(i) The weak assumption of exchangeable (rather than i.i.d.) scores allows to handle adaptive score training: the score functions can depend on the training sample, and on the calibration+test sample (in a way that maintains exchangeability).
(ii) Simultaneous and uniform inference: since m decisions are taken simultaneously (transductive setting), the joint error distribution should be taken into account for global risk assessment. We provide error bounds with high probability and uniform validity over a family of possible decisions (allowing for user or data-driven choice).
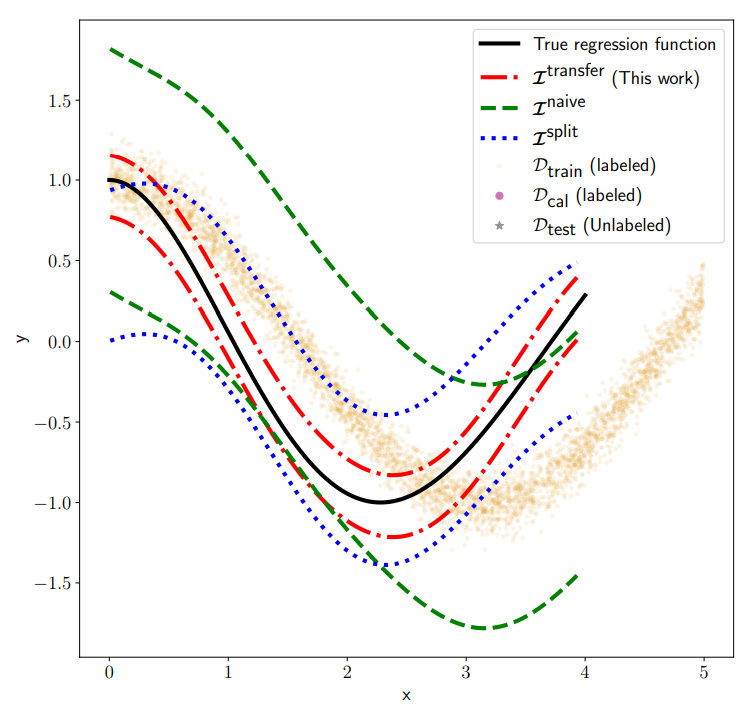
These findings are then applied in detail to (PI) in Section 3 and (ND) in Section 4. For (ND), we consider adaptive scores proposed by Marandon et al. (2022) leveraging two-class classification. For (PI), we consider a setting of domain shift between training and calibration+test, and introduce a novel approach (to our knowledge) of transductive transfer for PI, leveraging transfer learning algorithms. In both cases, use of adaptive scores significantly improves inference quality (see Figure 1 for our approach to transductive transfer PI). We give sharp bounds in probability for the false coverage proportion (FCP) (for PI) and the false discovery proportion (FDP) (for ND), with a possibly data-driven choice of the prediction intervals for (PI) and of the size of rejection threshold for (ND). This is in contrast to previous results only providing in-expectation guarantees of FCP/FDP. Our work hence brings more fine-grained reliability, which can be crucial when the practitioner faces sensible data.
1.3 Relation to previous work
For fundamentals on conformal prediction, see Vovk et al. (2005); Balasubramanian et al. (2014). We only consider the split conformal approach, also named inductive conformal approach in the seminal work of Papadopoulos et al. (2002). The split conformal approach uses a separate training set but is considered the most practically amenable approach for big data (in contrast to the “full conformal” approach which can be sharper but computationally intractable).
The most important consequence of score exchangeability is that the marginal distribution of a conformal p-value is a discrete uniform under the joint (calibration and test) data distribution. There has been significant recent interest for the conditional distribution of a marginal p-value, conditional to the calibration sample, under the stronger assumption of i.i.d. scores. The corresponding results take the form of bounds on P(p1 ≤ t|Dcal ) holding with high probability over Dcal (Vovk, 2012; Bian and Barber, 2022; Sarkar and Kuchibhotla, 2023; Bates et al., 2023, where in the two latter references the results are in addition uniformly valid in t). However, the i.i.d. scores assumption prevents handling adaptive scores (point (i) above), for which only exchangeability is guaranteed; moreover, these works are restricted to a single predictor, and do not address point (ii) either. Simultaneous inference for the (PI) task has been proposed by Vovk (2013) (see also Saunders et al., 1999 for an earlier occurrence for one p-value with multiple new examples), referred to as transductive conformal inference, and which includes a Bonferroni-type correction. Closest to our work, Marques F. (2023) analyzes the false coverage proportion (FCP) of the usual prediction interval family C(α) repeated over m test points: the exact distribution of the FCP under data exchangeability is provided, and related to a P`olya urn model with two colors. We show the more general result that the full joint distribution of (p1, . . . , pm) follows a P`olya urn model with (n+ 1) colors, which entails the result of Marques F. (2023) as a corollary (see Appendix A). This brings substantial innovations: our bounds on FCP are uniform in α, and we provide both the exact joint distribution and an explicit non-asymptotic approximation via a DKW-type concentration bound.
The (ND) setting is alternatively referred to as Conformal Anomaly Detection (see Chapter 4 of Balasubramanian et al., 2014). We specifically consider here the (transductive) setting of Bates et al. (2023) where the test sample contains novelties, and the corresponding p-values for ‘novelty’ entries are not discrete uniform but expected to be stochastically smaller. Due to strong connections to multiple testing, ideas and procedures stemming from that area can be adapted to address (ND), specifically by controlling the false discovery rate (FDR, the expectation of the FDP), such as as the Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg, 1995). Use of adaptive scores and corresponding FDR control has been investigated by Marandon et al. (2022). Our contribution with respect to that work comes from getting uniform and in-probability bounds for the FDP (rather than only in expectation, for the FDR).