Transductive Conformal Inference With Adaptive Scores: Main Results

Table of Links

• Abstract & Introduction
• Main results
• Application to prediction intervals
• Application to novelty detection
• Conclusion, Acknowledgements and References
• Appendix A: Exact formulas for Pn,m
• Appendix B: Numerical bounds and templates
• Appendix C: Proof
• Appendix D: Explicit control of (16) for α=0
• Appendix E: Proof of Corollary 4.1
• Appendix F: The Simes inequality
• Appendix G: Uniform FDP bound for AdaDetect
• Appendix H: Additional experiments

2 Main results

2.1 Setting

We denote integer ranges using JiK = {1, . . . , i}, Ji, jK = {i, . . . , j}. Let (Si)i∈Jn+mK be real random variables corresponding to non-conformity scores, for which (Sj )j∈JnK are the “reference” scores and (Sn+i)i∈JmK are the “test” scores. We assume

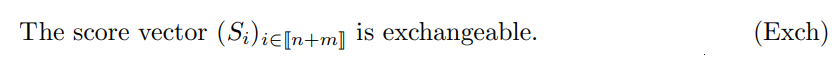
Under (Exch), the p-values (1) have super-uniform marginals (see, e.g., Romano and Wolf, 2005). In addition, the marginal distributions are all equal and uniformly distributed on {ℓ/(n + 1), ℓ ∈ Jn + 1K} under the additional mild assumption:

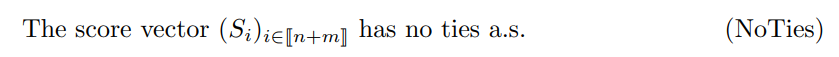
While the marginal distribution is well identified, the joint distribution of the p-values is not well studied yet. In particular, we will be interested in the empirical distribution function of the p-value family, defined as

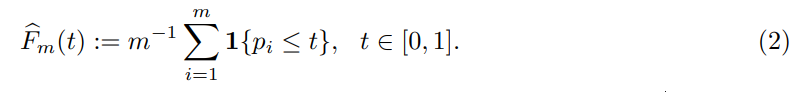
Note that the p-values are not i.i.d. under (Exch), so that most classical concentration inequalities, such as DKW’s inequality (Massart, 1990), or Bernstein’s inequality, cannot be directly used. Instead, we should take into account the specific dependence structure underlying these p-values.

2.2 Key properties

We start with a straightforward result, under the stronger assumption

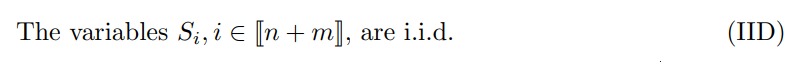
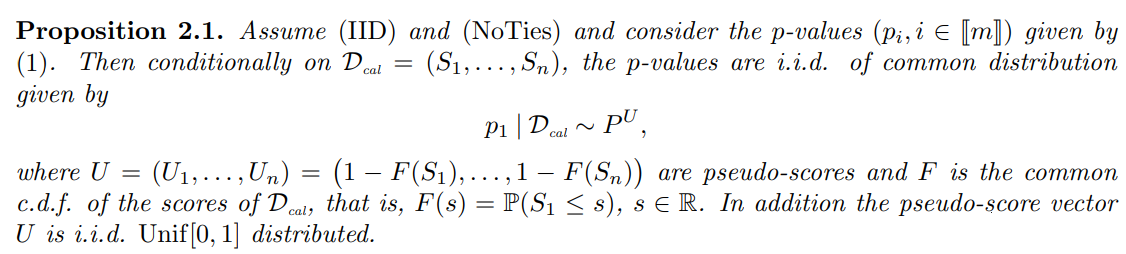
Proof sketch. The conditional distribution of pi only depends on score ordering which is unambiguous due to (NoTies), and is thus invariant by monotone transformation of the scores by (1 − F). Writing explicitly the cdf of pi from the uniformly distributed transformed scores yields (4). See Appendix C.1 for details.

In the literature, such a result is used to control the conditional failure probability P(p1 ≤ α| Dcal ) around its expectation (which is ensured to be smaller than, and close to, α) with concentration inequalities valid under an i.i.d. assumption (Bates et al., 2023; Sarkar and Kuchibhotla, 2023).

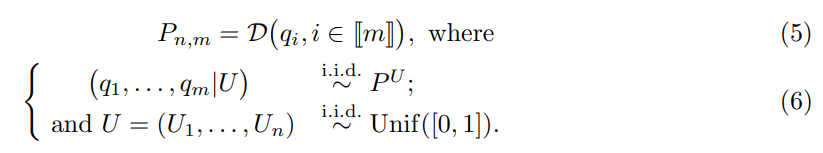
Proposition 2.2. Assume (Exch) and (NoTies), then the family of p-values (pi , i ∈ JmK) given by (1) has joint distribution Pn,m, which is defined by (5)-(6) and is independent of the specific score distribution.

The next proposition is an alternative and useful characterization of the distribution Pn,m.

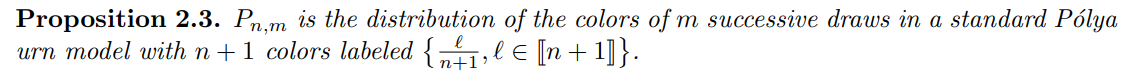
Proposition 2.3 is proved in Appendix A, where several explicit formulas for Pn,m are also provided. We also show that this generalizes the previous work of Marques F. (2023)

Comparing Proposition 2.1 and Proposition 2.2, we see that having i.i.d. scores is more favorable because guarantees are valid conditionally on Dcal (with an explicit expression for U = U(Dcal )). However, as we will see in Sections 3 and 4, the class of exchangeable scores is much more flexible and includes adaptive scores, which can improve substantially inference sharpness in specific situations. For this reason, we work with the unconditional distribution as in Proposition 2.2 in the sequel.

2.3 Consequences

We now provide a DKW-type envelope for the empirical distribution function (2) of conformal p-values. Let us introduce the discretized identity function

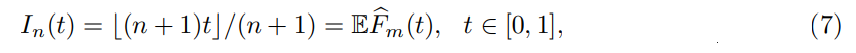
and the following bound:

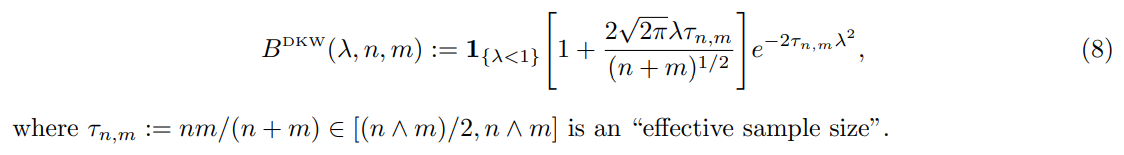
Proof sketch. Use the representation (6), apply the DKW inequality separately to (U1, . . . , Un) and to (q1, . . . , qm) conditional to U, and integrate over U. See Appendix C.4 for details (a slightly more accurate bound is also proposed).