This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ulysse Gazin, Universit´e Paris Cit´e and Sorbonne Universit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation,
(2) Gilles Blanchard, Universit´e Paris Saclay, Institut Math´ematique d’Orsay,
(3) Etienne Roquain, Sorbonne Universit´e and Universit´e Paris Cit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation.
Table of Links
- Abstract & Introduction
- Main results
- Application to prediction intervals
- Application to novelty detection
- Conclusion, Acknowledgements and References
- Appendix A: Exact formulas for Pn,m
- Appendix B: Numerical bounds and templates
- Appendix C: Proof
- Appendix D: Explicit control of (16) for α=0
- Appendix E: Proof of Corollary 4.1
- Appendix F: The Simes inequality
- Appendix G: Uniform FDP bound for AdaDetect
- Appendix H: Additional experiments
3 Application to prediction intervals
In this section, we apply our results to build simultaneous conformal prediction intervals, with an angle towards adaptive scores and transfer learning.
3.1 Setting

In addition, we consider the following transfer learning setting: while the data points are i.i.d. within each sample and the distributions of Dcal and Dtest are the same, the distribution of Dtrain can be different. However, Dtrain can still help to build a good predictor by using a transfer learning toolbox, considered here as a black box (see, e.g., Zhuang et al., 2020 for a survey on transfer learning). A typical situation of use is when the training labeled data Dtrain is abundant but there is a domain shift for the test data, and we have a limited number of labeled data Dcal from the new domain.
3.2 Adaptive scores and procedures



3.3 Transductive error rates
By Proposition 2.2, the following marginal control holds for the conformal procedure C(α) (13):
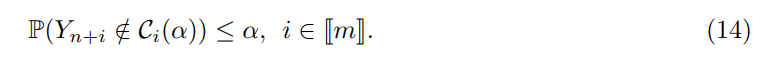
This is classical for non-adaptive scores and our result already brings an extension to adaptive scores in the transfer learning setting.
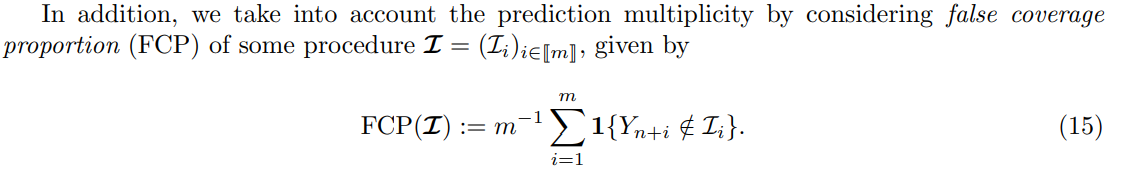



As a concrete example, one may want to choose a data-dependent αb to ensure prediction intervals C(α) of radius at most L, namely,
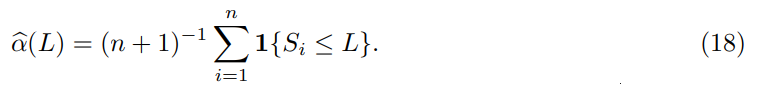
3.4 Controlling the error rates


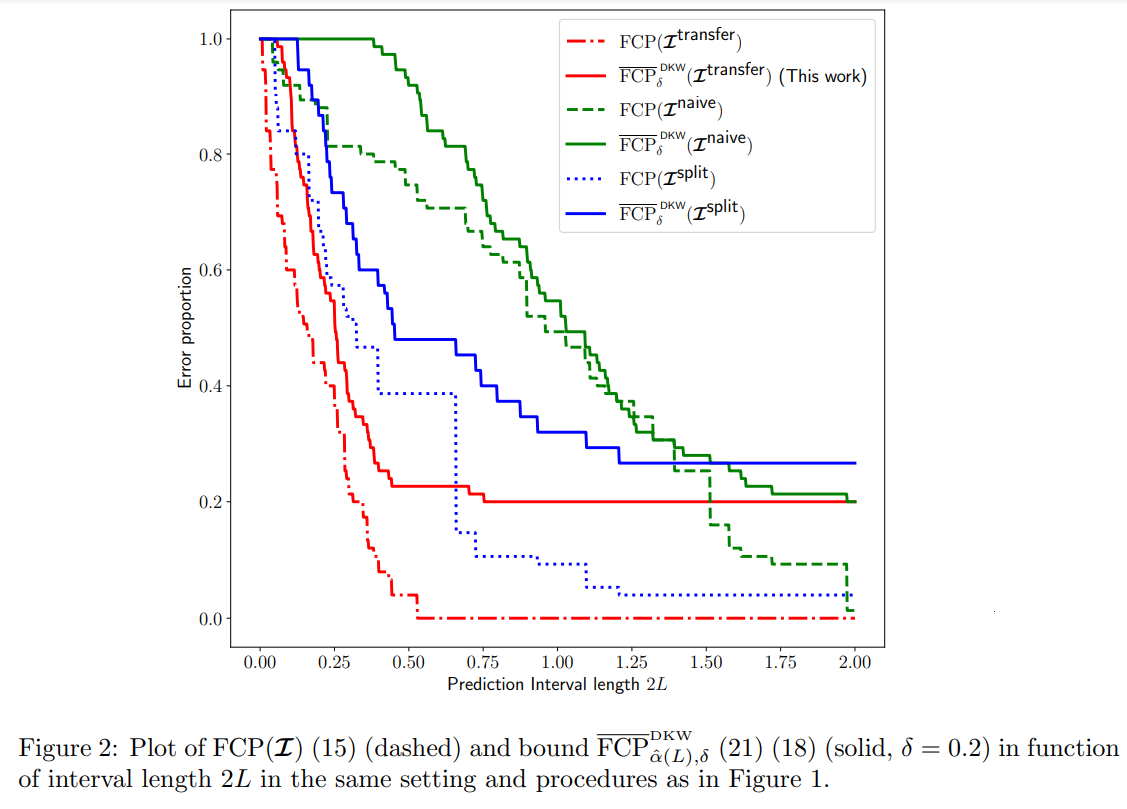
3.5 Numerical experiments