This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Pierre Colombo, Equall, Paris, France & MICS, CentraleSupelec, Universite Paris-Saclay, France;
(2) Victor Pellegrain, IRT SystemX Saclay, France & France & MICS, CentraleSupelec, Universite Paris-Saclay, France;
(3) Malik Boudiaf, ÉTS Montreal, LIVIA, ILLS, Canada;
(4) Victor Storchan, Mozilla.ai, Paris, France;
(5) Myriam Tami, MICS, CentraleSupelec, Universite Paris-Saclay, France;
(6) Ismail Ben Ayed, ÉTS Montreal, LIVIA, ILLS, Canada;
(7) Celine Hudelot, MICS, CentraleSupelec, Universite Paris-Saclay, France;
(8) Pablo Piantanida, ILLS, MILA, CNRS, CentraleSupélec, Canada.
Table of Links
- Abstract & Introduction
- Related Work
- API-based Few-shot Learning
- An Enhanced Experimental Setting
- Experiments
- Conclusions
- Limitations, Acknowledgements, & References
- Appendix A: Proof of Proposition
- Appendix B: Additional Experimental Results
A Proof of Proposition

Lemma 1. For any arbitrary r.v. X and countable r.v. Y , we have
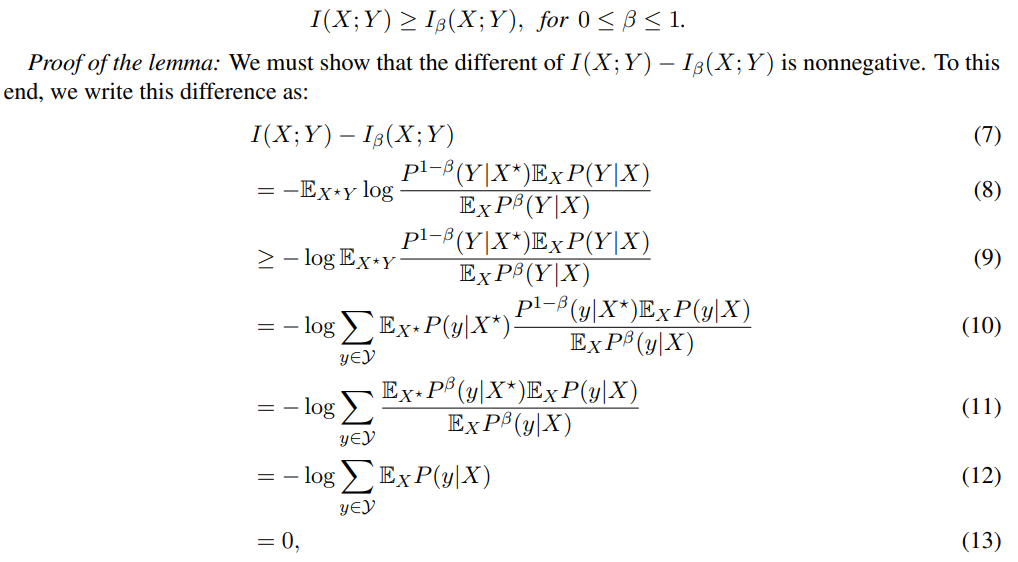
where the first inequality follows by applying Jensen’s inequality to the function t 7→ − log(t).
Proof of Proposition 1: From Lemma 1, using Jensen’s inequality, we have
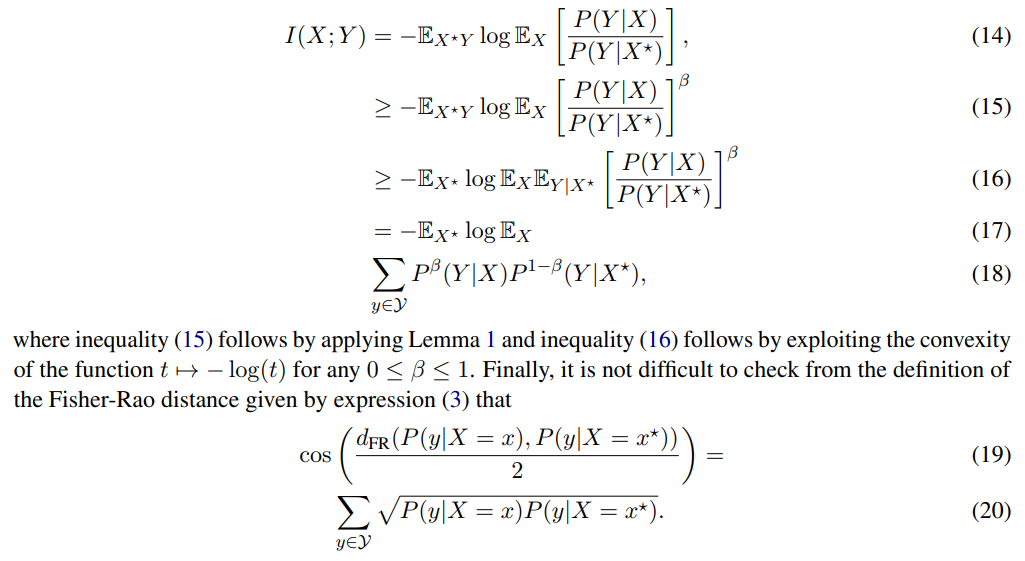
Using the identity given by (19) in expression (18), and setting β = 1/2, we obtain the following lower bound on I(X; Y ):
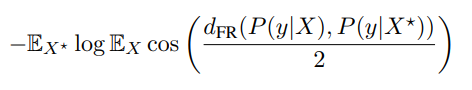
The inequality (6) immediately follows by replacing the distribution of the r.v. X with the empirical distribution on the query and P(y|x) with the soft-prediction corresponding to the feature x, which concludes the proof of the proposition.

