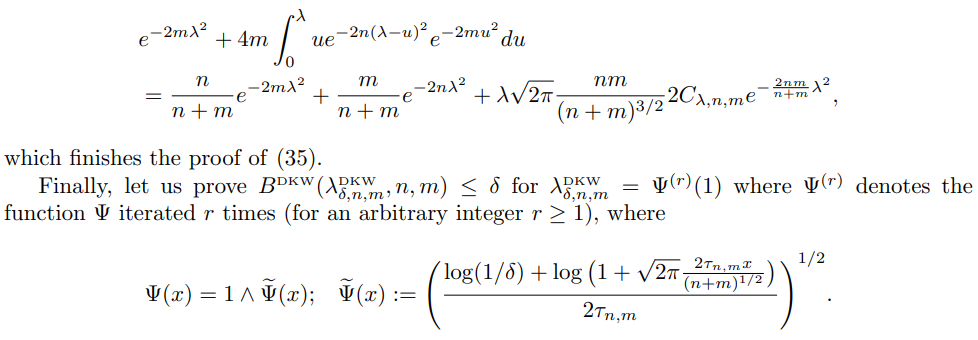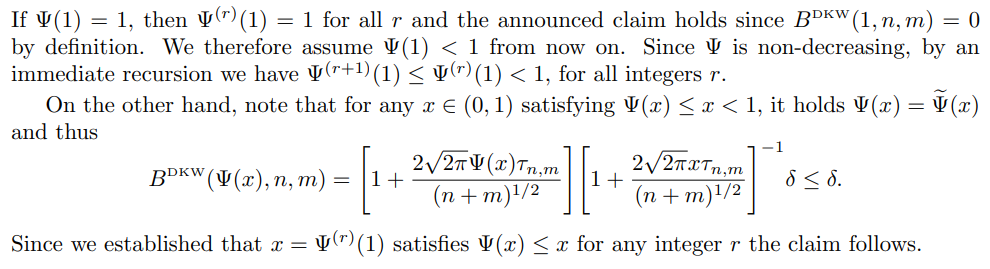This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ulysse Gazin, Universit´e Paris Cit´e and Sorbonne Universit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation,
(2) Gilles Blanchard, Universit´e Paris Saclay, Institut Math´ematique d’Orsay,
(3) Etienne Roquain, Sorbonne Universit´e and Universit´e Paris Cit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation.
Table of Links
- Abstract & Introduction
- Main results
- Application to prediction intervals
- Application to novelty detection
- Conclusion, Acknowledgements and References
- Appendix A: Exact formulas for Pn,m
- Appendix B: Numerical bounds and templates
- Appendix C: Proof
- Appendix D: Explicit control of (16) for α=0
- Appendix E: Proof of Corollary 4.1
- Appendix F: The Simes inequality
- Appendix G: Uniform FDP bound for AdaDetect
- Appendix H: Additional experiments
C Proofs
C.1 Proof of Proposition 2.1
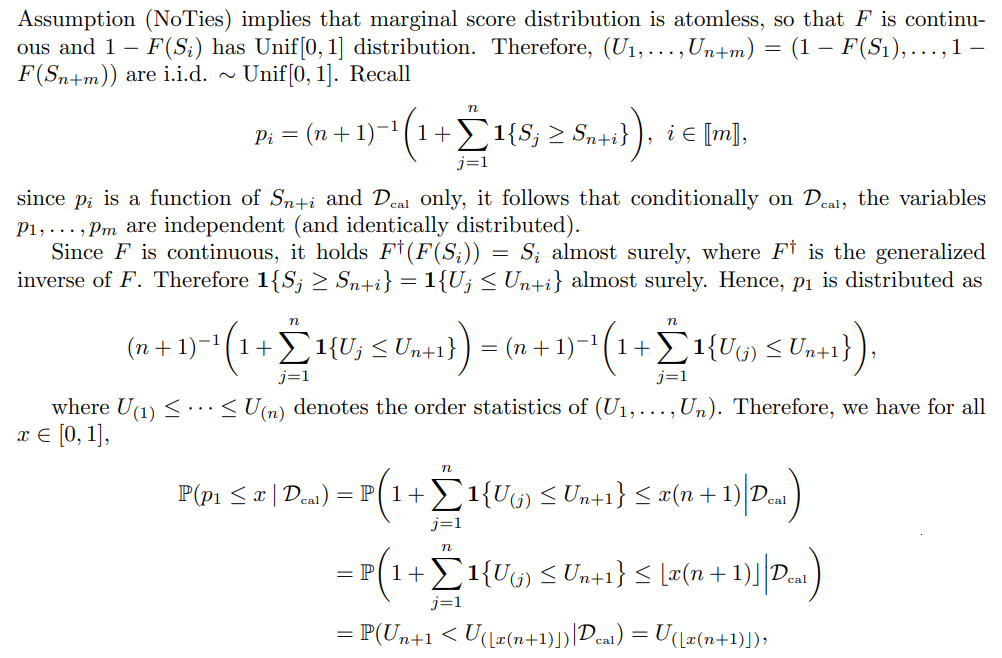
which finishes the proof.
C.2 Proof of Proposition 2.2
If there are no tied scores, which by assumption (NoTies) happens with probability 1, the ranks Ri of the ordered scores are well-defined and the vector (p1, . . . , pm) is only a function of the rank vector (R1, . . . , Rn+m). Namely, Ri ≤ Rj if and only if Si ≤ Sj , and the conformal p-values (1) can be written as
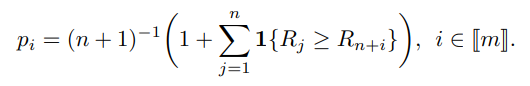

C.3 Proof of Theorem A.1
Proof of (ii) By (Exch),(NoTies) the permutation that orders the scores (S1, . . . , Sn+m) that is σ such that

This event can be formally described as follows:
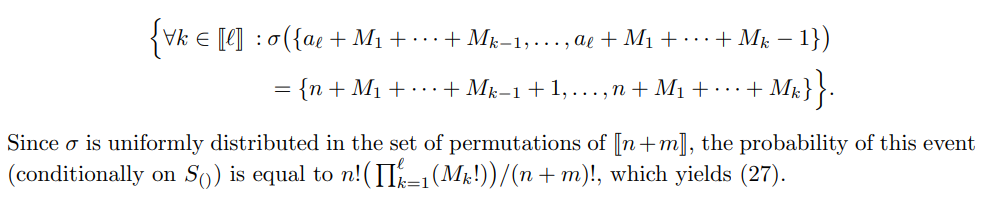
Proof of (i) By using (27) of (ii), we have
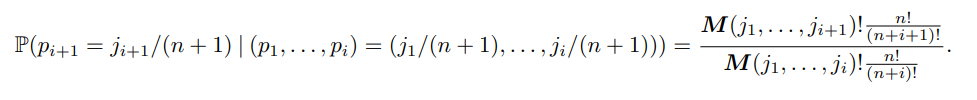
Now, we have
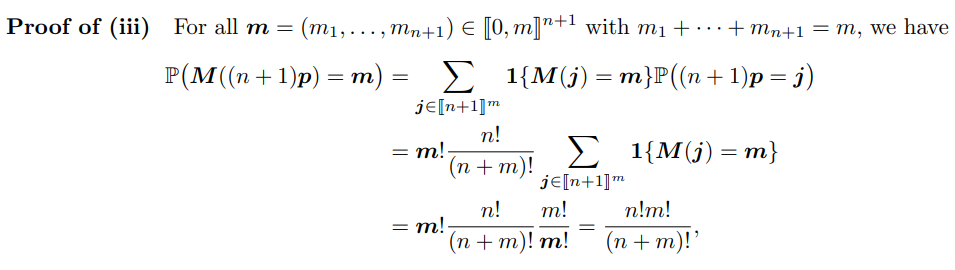
where we have used (ii) and the multinomial coefficient
C.4 Proof of Theorem 2.
First observe that the LHS of (9) is 0 if λ ≥ 1 so that we can assume λ < 1
Let us prove (9) with the more complex bounce
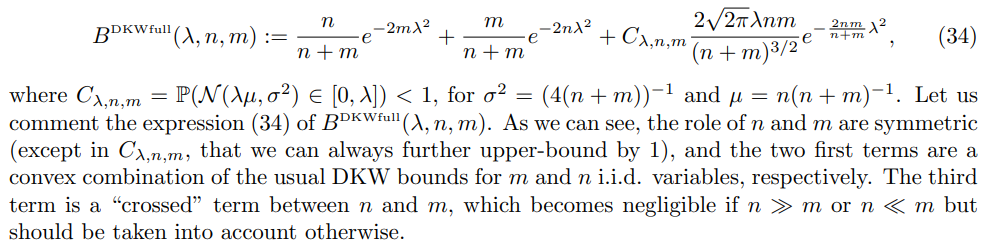
Below, we establish


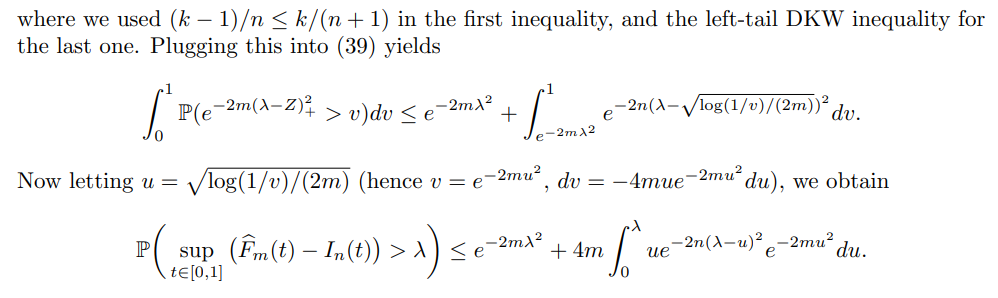
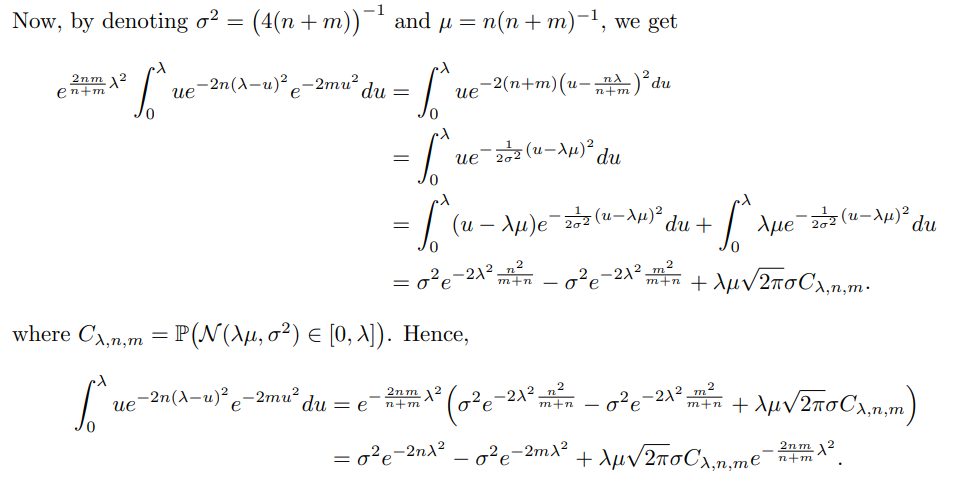
This leads to