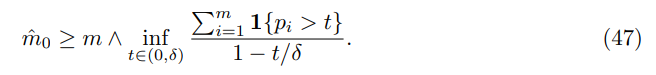This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ulysse Gazin, Universit´e Paris Cit´e and Sorbonne Universit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation,
(2) Gilles Blanchard, Universit´e Paris Saclay, Institut Math´ematique d’Orsay,
(3) Etienne Roquain, Sorbonne Universit´e and Universit´e Paris Cit´e, CNRS, Laboratoire de Probabilit´es, Statistique et Mod´elisation.
Table of Links
- Abstract & Introduction
- Main results
- Application to prediction intervals
- Application to novelty detection
- Conclusion, Acknowledgements and References
- Appendix A: Exact formulas for Pn,m
- Appendix B: Numerical bounds and templates
- Appendix C: Proof
- Appendix D: Explicit control of (16) for α=0
- Appendix E: Proof of Corollary 4.1
- Appendix F: The Simes inequality
- Appendix G: Uniform FDP bound for AdaDetect
- Appendix H: Additional experiments
F The Simes inequality
As proved in Marandon et al. (2022), and since the joint distribution of the conformal p-values does not change from one context to another (Proposition 2.2), the conformal p-values are positively regressively dependent on each one of a subset (PRDS) under (Exch) and (NoTies), see Benjamini and Yekutieli (2001) for a formal definition of the latter.
Hence, by Benjamini and Yekutieli (2001), the Simes inequality (Simes, 1986) is valid, that is, for all λ > 0, we have
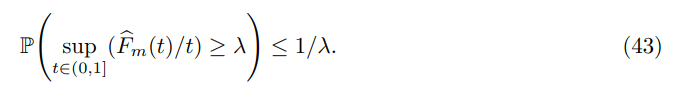
This envelope can be applied in the two applications of the paper as follows:
(PI) Under the condition of Corollary 3.1, the bound
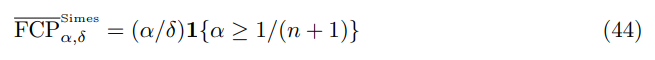
is valid for (17).
(ND) Under the condition of Corollary 4.1 the following control is valid
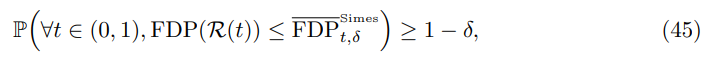
for

for any estimator