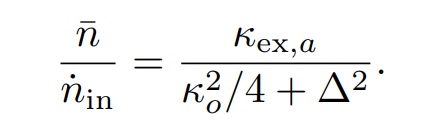This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Terence Blésin, Institute of Physics, Swiss Federal Institute of Technology Lausanne (EPFL) & Center of Quantum Science and Engineering (EPFL);
(2) Wil Kao, Institute of Physics, Swiss Federal Institute of Technology Lausanne (EPFL) & Center of Quantum Science and Engineering (EPFL);
(3) Anat Siddharth, Institute of Physics, Swiss Federal Institute of Technology Lausanne (EPFL) & Center of Quantum Science and Engineering (EPFL);
(4) Alaina Attanasio, OxideMEMS lab, Purdue University;
(5) Hao Tian, OxideMEMS lab, Purdue University;
(6) Sunil A. Bhave, OxideMEMS lab, Purdue University;
(7) Tobias J. Kippenberg, Institute of Physics, Swiss Federal Institute of Technology Lausanne (EPFL) & Center of Quantum Science and Engineering (EPFL).
Table of Links
-
Results
II. RESULTS
A. Physics and design
Figure 1 delineates the principle of operation of the present transducer, while the theoretical formalism is detailed in Appendix A. The requisite nonlinear interaction for microwave-optical transduction is a parametric threewave mixing process described by standard optomechanical Hamiltonian
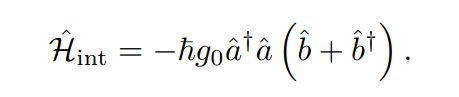
Through the bilinear piezoelectric interaction, the acoustic resonance (ˆb) is coupled to the itinerant transmission line mode (cˆin) of the same frequency ωin = ωm ≈ 3.5 GHz. This frequency matches the detuning of the optical pump from the optical resonance (aˆ). Specifically, an optical pump addressing the red (blue) side of the resonance induces an effective beam-splitter (two-modesqueezing) interaction between aˆ and ˆb, as illustrated by the signal flow graph in Fig. 1a (1b). The primary figure of merit for a transducer is its efficiency, defined as the number of output photon number for each input photon. An efficient device necessitates strong nonlinear interaction between the modes of interest, as well as ease of coupling to these modes internal to the device. Our design addresses these two aspects. First, the internal efficiency,
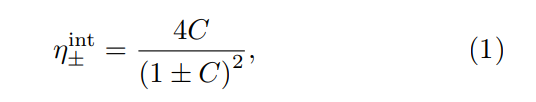
depends solely on the three-wave mixing cooperativity C = 4g 2 0n/¯ (κoκm). Here, n¯, κo, and κm denote the photon number in the optical cavity, and the total optical and acoustic linewidths of the transduction modes respectively. The single photon optomechanical coupling rate g0 = − (∂ωa/∂x) xZPF, a product of the optical cavity frequency-pull parameter and zero-point displacement of the acoustic wave. In Eq. 1, the plus and minus signs in the denominator correspond to the scenario where the pump is red- and blue-detuned (“anti-Stokes” and “Stokes” processes), respectively. Using a triply resonant configuration as in Refs. [26–29] enhances the intracavity photon number n¯ for a given off-chip input pump power Pin, or corresponding photon flux n˙ in = Pin/ (ℏωL). The improved photon pumping efficiency can be explicitly seen by considering a “hot” cavity with coupling rate κex,o driven at a detuning ∆ = ±ωm, yielding